Pythagorova věta: Nepostradatelný matematický vzorec pro vzdělání

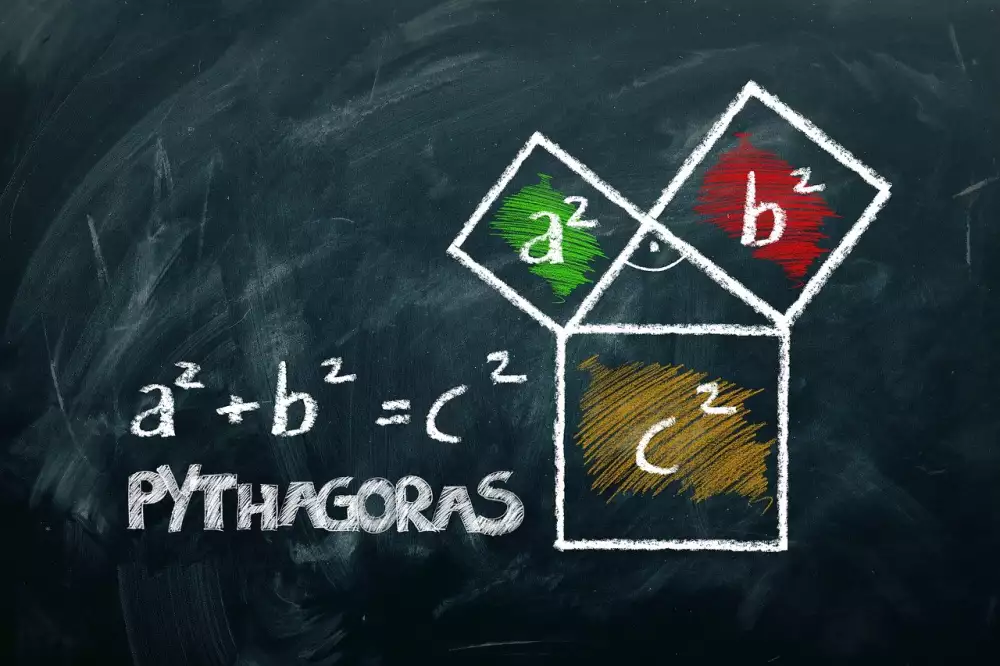
Úvod do Pythagorovy věty

Pythagorova věta je základním matematickým vzorcem, který se používá k výpočtu délky nejdelší strany pravoúhlého trojúhelníka. Tento vzorec byl objeven starověkým řeckým filozofem Pythagorou a dodnes patří mezi nejdůležitější matematické teorie. Podle Pythagorovy věty platí, že druhá mocnina délkami přepony (nejdelší strany) je rovna součtu druhých mocnin délek obou odvěsen trojúhelníka. Konkrétně tedy vzorec zní: c^2 = a^2 + b^2. Tento vzorec lze aplikovat na různé situace - například ke výpočtu délky stínítka při umístění slunečních panelů, kdy musíme správně odhadnout velikost trojúhelníku tvořeného sluncem, panelem a stínítkem. Pythagorova věta má tedy široké uplatnění jak v matematice, tak i ve fyzice či technických oborech.

Historické pozadí Pythagorovy věty

Historie pythagorovy věty sahá až do starověkého Řecka, kde byl Pythagoras znám jako filozof, matematik a mystik. Jeho jméno bývá nejčastěji spojováno právě s touto slavnou větou, která se stala jedním z nejznámějších matematických vzorců. Byla objevena již dávno před Pythagorem, avšak jemu je přisuzován její dokonalý důkaz. Tento vzorec umožňuje určit délku strany pravoúhlého trojúhelníka pomocí délek jeho zbývajících dvou stran a vyjadřuje tak základní geometrický princip. Pythagorova věta má proto velký význam nejen pro matematiku, ale i pro technické a inženýrské obory, kde se často používá k výpočtům délek a rozměrů různých konstrukcí.

Vysvětlení Pythagorovy věty

Pythagorova věta je matematický vzorec, který se týká pravoúhlého trojúhelníka. V podstatě jde o tvrzení, že druhá mocnina délky nejdelší strany (tzv. přepony) je rovna součtu druhých mocnin délek zbývajících dvou stran (tzv. odvěsen). Tento vztah lze zapsat formálně jako a² + b² = c², kde 'a' a 'b' označují délky odvěsen a 'c' přepony.

Pythagorova věta se používá nejenom v matematice, ale také v řadě dalších oblastí jako fyzika, geodézie či architektura. Je to jeden z nejdůležitějších vzorců v geometrii a jeho pochopení je klíčové pro mnoho dalších matematických konceptů.

Matematický vzorec Pythagorovy věty

Matematický vzorec Pythagorovy věty patří mezi základní pojmy z oblasti geometrie. Tento vzorec, pojmenovaný po starověkém řeckém matematikovi Pythagorasovi, umožňuje spočítat délku přepony pravoúhlého trojúhelníka na základě délek jeho odvěsen. Konkrétně se jedná o souvislost mezi čtverci délek odvěsen a čtvercem délky přepony. Matematický vzorec Pythagorovy věty zní: c² = a² + b², kde c je délka přepony a a,b jsou délky odvěsen. Tento vzorec nachází široké využití nejen v matematice, ale i v technických oborech a dalších vědních disciplínách, které se zabývají geometrií.

Příklady použití Pythagorovy věty

Pythagorova věta je matematický vzorec, který říká, že ve trojúhelníku s pravoúhlým úhlem (tzv. pravoúhlém trojúhelníku) platí: Součet druhých mocnin odvěsen (tj. stran trojúhelníku ležících proti pravoúhlému úhlu) je roven druhé mocnině přepony (tj. strany protilehlé k pravoúhlému úhlu). Tento vzorec nachází své uplatnění v mnoha oblastech matematiky a fyziky. Například se používá při výpočtu délek diagonál čtyřstěnů, vzdálenostech planet od Slunce nebo určení vzdálenosti slyšených zvuků při měření akustických parametrů prostoru. Pythagorova věta je také klíčovým prvkem pro pochopení trigonometrických funkcí, což umožňuje mnoho dalších aplikací v různých oblastech, jako jsou např. stavba mostů a budov nebo rozmístění antén pro bezdrátovou komunikaci.

Význam Pythagorovy věty ve vzdělání

Pythagorova věta patří mezi základní matematické vzorce a je důležitým prvkem v mnoha oborech, zejména ve vzdělání. Jejím významem je umožnit výpočty a měření úhlů a rozměrů v různých geometrických tvarech, jako jsou trojúhelníky, čtverce a obdélníky. Díky Pythagorově větě mohou studenti lépe pochopit koncept hypoténusy, což je nejdůležitější strana trojúhelníka. Vyučování Pythagorovy věty také rozvíjí matematické myšlení a schopnosti řešení problémů. Navíc je Pythagorova věta velmi užitečná pro reálné aplikace, například při návrhu budov, stavebnictví a technických oborech. Proto lze říci, že znalost Pythagorovy věty má nezastupitelný význam ve vzdělání souvisejícím s matematikou i praktickými obory.

Závěr a využití Pythagorovy věty v praxi

Závěr a využití Pythagorovy věty v praxi je neobyčejně široké téma, které nachází uplatnění nejen v matematice, ale i ve fyzice, geodézii či architektuře. Pythagorova věta umožňuje spočítat délky stran pravoúhlých trojúhelníků, avšak toto pravidlo se dá aplikovat i mnoha jinými způsoby. Například se s ním pracuje při návrhu schodišť, stavebních konstrukcí a pro vytyčování diagonál ploch. Dále se tato věta používá například také při měření vzdáleností mezi body na zemském povrchu (geodézie) nebo při řešení úloh o rychlosti auta na silnici (fyzika). Shrnuto lze říci, že Pythagorova věta patří mezi základy matematických poznatků a její aplikace jsou bezpočetné a týkající se mnoha odvětví lidského života.